Cap. 6 - Funciones fructíferas (que retornan un valor)

6.1) Valores de retorno

Las funciones built-in que hemos usado (como abs, pow, int, max y range) devuelven resultados. El llamado a una de estas funciones produce un valor que solemos asignar a una variable, o que usamos como parte de una expresión.

		mayor = max(3, 2, 5, 7)
		x = abs(3 - 11) * 10

También escribimos nuestra propia función para calcular y devolver el monto final para un capital puesto a interés compuesto.

En este capítulo escribiremos más funciones que retornan valores, las que hemos llamado funciones fructíferas a falta de un nombre mejor. El primer ejemplo es area, (L6_funcion_area.py) que calcula el área de un círculo de radio dado:

		def area(radio):
		    b = 3.14159 * radio ** 2
		    return b

Ya habíamos visto la sentencia return, pero en una función fructífera ésta siempre incluye un valor de retorno. La sentencia significa: evaluar la expresión de retorno, y luego devolverla ese valor como el resultado (o fruto) de la función. La expresión puede ser arbitrariamente complicada, por lo cual podríamos haber definido la función así: (L6_funcion_area.py)

		def area(radio):
		    return 3.14159 * radio ** 2

De todas formas, variables temporales como la b del ejemplo anterior simplifican las tareas de debugging.

En algunos casos es útil tener varias sentencias return, una en cada rama de una sentencia condicional. Veamos por ejemplo cómo escribir nuestra propia versión de la función valor_absoluto: (L6_funcion_area.py)

		def valor_absoluto(x):
		    if x < 0:
		        return -x
		    else:
		        return x

También se podría haber eliminado el cláusula else y simplemente hacer que la sentencia if fuera seguida por un return, así: (L6_funcion_area.py)

		def valor_absoluto(x):
		    if x < 0:
		        return -x
		    return x

Vale la pena pensar en esta segunda versión un tiempo para convencerse de que hace exactamente lo mismo que la primera.

Se llama código muerto o código inalcanzable al código que está después de una sentencia return o en un lugar que el flujo de ejecución nunca puede alcanzar.

En una función fructífera, es una buena idea asegurar que todo camino posible a través del programa alcance una sentencia return. La siguiente versión de valor_absoluto (L6_funcion_area.py) falla en cumplir dicho objetivo:

		def valor_absoluto_mal_definido(x):
		    if x < 0:
		        return -x
		    elif x > 0:
		        return x

Esta versión no es correcta porque si x == 0, ninguna de las dos condiciones es verdadera y la función termina sin alcanzar un enunciado return. En tal caso, el valor retornado es None.

		>>> print(valor_absoluto_mal_definido(0))
		None

Todas las funciones Python retornan None cuando se ven en la situación de terminar sin haber retornado otro valor.

También es posible usar un return en el medio de un loop for, en cuyo caso el control retorna de inmediato de la función. Supongamos que queremos una función que busque en una lista de palabras y que retorne la primera palabra de 2 letras que encuentre. Si no encuentra ninguna, debe retornar el string vacío. (L6_funcion_area.py)

		def encontrar_primer_palabra_de_dos_letras(xs):
		    for wd in xs:
		        if len(wd) == 2:
		            return wd

		    return ""

		>>> encontrar_primer_palabra_de_dos_letras(["Este", "es", "un", "loro", "muerto"])
		'es'
		>>> encontrar_primer_palabra_de_dos_letras(["Pienso", "luego", "existo"])
		''

En el primero de los ejemplos anteriores, la función retorna antes de completar el loop for (no tiene que seguir recorriendo la lista una vez que encontró el primer caso favorable). En cambio en el segundo ejemplo recorre la lista completa porque no encuentra ningún caso.

6.2) Desarrollo de un programa

En este momento deberías ser capaz de mirar el código de funciones completas y poder decir qué es lo que hacen. Si estuviste haciendo los ejercicios, ya habrás escrito algunas pequeñas funciones. A medida que escribas funciones más largas irán surgiendo nuevas dificultades, especialmente errores de tiempo de ejecución y errores semánticos.

Para lidiar con programas de complejidad creciente, utilizaremos la técnica llamada desarrollo incremental. El objetivo es evitar largas sesiones de debugging mediante la adición y testeo inmediato de pequeñas cantidades de código en cada paso.

Por ejemplo, supongamos que queremos calcular la distancia entre dos puntos, dados por las coordenadas (x1, y1) y (x2, y2). Por el teorema de Pitágoras, la distancia es:

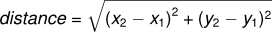
El primer paso es considerar cómo se vería una función distancia se vería en Python. En otra palabras, cuál sería el input y cuál sería el output?

En este caso, los dos puntos son el input, lo que corresponde a 12 parámetros. La distancia es un floating, que será el valor de retorno.

Podemos escribir un esbozo de la función que captura lo que hemos dicho hasta ahora: (L6_funcion_area.py)

		def distancia(x1, y1, x2, y2):
		    return 0.0

Obviamente, esta versión de la función no computa la distancia. Pero es sintácticamente correcta y retorna un valor, lo que significa que podemos irla adaptando hasta hacerla cumplir lo que queremos.

Para testear la nueva función, la llamamos con valores concretos:

		>>> distancia(1, 2, 4, 6)
		0.0

Elegimos estos valores para que la distancia horizontal sea 3 y la vertical sea 4. De este modo, el resultado será 5 (hipotenusa del triángulo 3-4-5). Al testear una función es útil saber de antemano la respuesta que esperamos.

En este punto ya sabemos que la función es sintácticamente correcta, y podemos comenzar a agregar líneas de código. A cada cambio volvemos a testear la función. Si ocurre un error en cualquier punto, sabemos dónde debe estar: en la última línea que hemos agregado.

Un primer paso lógico es calcular las diferencias x2 - x1 e y2 - y1, las cuales llamaremos dx y dy respectivamente. (L6_funcion_area.py)

		def distancia(x1, y1, x2, y2):
		    dx = x2 - x1
		    dy = y2 - y1
		    return 0.0

Si llamamos a la función con los argumentos mostrados arriba, en el momento en que el flujo de ejecución alcanza a la sentencia return, las variables dx y dy deberían valer 3 y 4 respectivamente. Podemos testearlo en PyScripter poniendo el cursor en la línea return y ejecutando el programa para que se interrumpa en la línea return (utilizando la tecla F4, instrucción Run > Run to cursor). Entonces podemos chequear los valores de dx y dy con poner el puntero del mouse sobre dichas variables. Esto nos permite confirmar que la función esté recibiendo los parámetros correctos y esté haciendo los cálculos correctamente. Si no es así, sólo tenemos que revisar unas pocas líneas.

Luego computamos la suma de los cuadrados de dx y dy: (L6_funcion_area.py)

		def distancia(x1, y1, x2, y2):
		    dx = x2 - x1
		    dy = y2 - y1
		    ds_al_cuadrado = dx*dx + dy*dy
		    return 0.0

Una vez más, podríamos correr el programa ahora y chequear si ds_al_cuadrado vale 25 en el momento en que se alcanza la línea return.

Finalmente, utilizando el exponente fraccionario 0.5 para calcular la raíz cuadrada, computamos y retornamos el resultado: (L6_funcion_area.py)

		def distancia(x1, y1, x2, y2):
		    dx = x2 - x1
		    dy = y2 - y1
		    ds_al_cuadrado = dx*dx + dy*dy
		    distancia = ds_al_cuadrado ** 0.5
		    return distancia

Si funciona bien, hemos terminado. En caso contrario, habrá que inspeccionar el valor de la variable distancia justo antes de ejecutar la sentencia return.

Cuando comienzas a programar, conviene que agregues código de a una línea o dos. A medida que ganes experiencia, terminarás programando y haciendo debugging de trozos mayores de código en cada etapa. En ambos casos, ejecutar el programa línea por línea y verificar que las variables estén cambiando como esperabas (con un ejemplo concreto bien conocido) puede ahorrarte mucho tiempo de debugging. A medida que mejores tu habilidad como programador serás capaz de manejar trozos más grandes de código en cada etapa. Es algo similar al modo en que aprendimos a leer letras, sílabas, palabras, frases, párrafos, etc., o el modo en que aprendemos a subdividir la música (desde nota por nota a acordes, compases, motivos, etc.)

Los aspectos claves del proceso son:

Comenzar con un esqueleto que funciona e ir haciendo pequeños cambios incrementales. En cada punto, si hay un error, sabrás exactamente dónde puede estar.
Usar variables temporales para referirse a valores intermedios para que sea fácil inspeccionarlos
Una vez que el programa funcione, conviene relajarse y probar a hacerle pequeños cambios para mejorarlo. "Jugar" con cambios y variantes siempre es productivo en cualquier actividad.
- Puedes por ejemplo combinar varias sentencias en una expresión compuesta mayor, o cambiarle el nombre a las variables, o ver si se puede escribir una versión más corta de la función
- Una buena regla de trabajo es tratar de hacer el código fácil de leer y de comprender para otras personas

Aquí tenemos otra versión de la función distancia. (L6_funcion_area.py) Utiliza la función sqrt del módulo math (aprenderemos más sobre los módulos en breve). ¿Cuál prefieres? ¿Cuál se parece más a la fórmula pitagórica inicial?

		def distancia_math(x1, y1, x2, y2):
		    return math.sqrt( (x2-x1)**2 + (y2-y1)**2 )

6.3) Debugging con PRINT

Otra forma práctica de hacer debugging (alternativa a la ejecución paso a paso) es insertar sentencias print extras en lugares cuidadosamente seleccionados. Luego, inspeccionando el output del programa, se puede chequear si el algoritmo está haciendo lo que queremos. Sin embargo, hay que tener en cuenta lo siguiente:

Es necesario tener una solución clara del problema, y es necesario saber qué debería pasar antes de hacer debugging. Primero conviene resolver el problema en una hoja de papel (tal vez utilizando un diagrama de flujo para comprender bien sus pasos) antes de ponerse a escribir código. Escribir un programa no resuelve el problema - simplemente automatiza los pasos manuales que hubiéramos realizado en la hoja de papel. Así que lo primero es asegurarse que nuestra solución funciona con lápiz y papel. Programar consiste entonces en convertir esos pasos manuales en acciones automáticas.
No conviene escribir funciones charlatanas (chatterbox). Una función charlatana es una función fructífera que, además de su tarea principal (que es devolver un valor), también pide al usuario que ingrese inputs, e imprime outputs, cuando sería mucho mejor si simplemente hiciera su trabajo con la boca bien cerrada.

Por ejemplo, hemos visto funciones built-in como max, range y abs. Ninguna de éstas sería un bloque útil para otro programa si pidiera al usuario un input o imprimiera sus resultados intermedios a medida que ejeucta la tarea.

Por lo tanto, una buena recomendación es evitar llamar a print o a input dentro de funciones fructíferas, a menos que el propósito primario de dicha función sea realizar ese input y output. La única excepción sería intercalar prints (e incluso inputs) temporales en nuestro código para ayudar al debug y comprender qué está pasando cuando se ejecuta el programa, pero esos prints serán borrados cuando el programa ya funcione.

6.4) Composición

Como era de esperar, puedes llamar a una función desde otra. Esta capacidad se conoce como composición.

Como ejemplo, escribiremos una función que recibe dos puntos, el centro del círculo y un punto del perímetro, y calcula el área del círculo.

Supongamos que las coordenadas del centro se reciben en los parámetros xc e yc y el punto del perímetro en los xp e yp´. El primer paso es encontrar el radio, que es la distancia entre los dos puntos. Acabamos de escribir la función distancia que hace esto, así que podemos usarla:

		radio = distancia(xc, yc, xp, yp)

El segundo paso es encontrar el área del círculo para dicho radio y devolverla. Otra vez utilizamos una función que ya implementamos, la función area:

		resultado = area(radio)
		return resultado

Poniendo todo en una función, obtenemos: (L6_funcion_area.py)

		def area2(xc, yc, xp, yp):
		    radio = distancia(xc, yc, xp, yp)
		    resultado = area(radio)
		    return resultado

Llamamos a esta función area2 para distinguirla de la función area que habíamos definido antes.

Las variables temporales radio y resultado son útiles para el desarrollo, el debugging y el testeo paso a paso, pero una vez que el programa ya funciona, se puede hacer una versión más concisa por composición de los llamados a funciones, así: (L6_funcion_area.py)

		def area2(xc, yc, xp, yp):
		    return area(distancia(xc, yc, xp, yp))

6.5) Funciones booleanas

Se llama así a las funciones que retornan valores booleanos. Permiten ocultar tests complicados dentro de una función. Por ejemplo: (L6_funcion_area.py)

		def es_divisible(x, y):
		    """ Verifica si x es exactamente divisible por y """
		    if x % y == 0:
		        return True
		    else:
		        return False

Es común dar a las funciones booleanas nombres que suenan como preguntas sí/no. La función es_divisible retorna True o False para indicar si x es o no es divisible por y.

Podemos hacer a la función más concisa si aprovechamos el hecho de que la condición del if es en sí misma una expresión booleana. Por lo cual la podemos retornar como resultado: (L6_funcion_area.py)

		def es_divisible(x, y):
		    """ Verifica si x es exactamente divisible por y """
		    return x % y == 0

Aquí vemos 3 ejemplos de output:

		>>> es_divisible(6, 4)
		False
		>>> es_divisible(6, 3)
		True
		>>> es_divisible(6.2, 3)
		False
		>>> es_divisible(6.2, 3.1)
		True

Observación: el operador módulo (%) funciona también para números float. Su significado corresponde a devolver el resto de la división entre los dos números, exactamente como cuando se opera entre enteros. Revisar bien la definición del operador módulo para floats.

Las funciones booleanas son usadas frecuentemente en enunciados condicionales:

		if es_divisble(x, y):
			... # Hacer algo ...
		else:
			... # Hacer otra cosa ...

Uno podría pensar en escribir algo así:

		if es_divisible(x, y) == True:

Pero la comparación extra es innecesaria (no es incorrecta, pero está de más).

6.6) Programando con estilo

La legibilidad (readability) es muy importante para los programadores, ya que en la práctica los programas son leídos y modificados muchas más veces que las que son creados. Sin embargo, como con todas las reglas, muchas veces ésta no se cumple. Muchos de los ejemplos de código en este curso son consistentes con el PEP 8 (Python Enhancemente Proposal 8) (http://www.python.org/dev/peps/pep-0008/), una guía de estilo desarrollada por la comunidad Python.

Tendremos más que decir sobre estilo a medida que nuestros programas se vayan volviendo más complejos, pero los puntos principales son estos:

Usar 4 espacios (en vez de tabulaciones) para las indentaciones
Limitar el largo de una línea a 78 caracteres
En los nombres de identificadores, usar CamelCase para clases (a las que ya llegaremos) y minusculas_con_infraguiones para funciones y variables
Ubicar los import en el top del archivo
Poner las definiciones de funciones todas juntas
Usar docstrings para documentar funciones
Usar dos líneas en blanco para separar una definición de función de otra
Mantener a los enunciados de máximo nivel (top level), incluyendo a los llamados a función, juntos y en las líneas finales del programa

6.7) Testeo de unidades

Es una buena práctica de desarrollo de software el incluir un testeo de unidad (unit testing) automático del código fuente. El testeo de unidades provee de una forma de verificar automáticamente que las piezas de código individual (como las funciones) estén funcionando bien. Esto permite modificar la implementación de una función en el futuro y testear entonces, rápidamente, si todavía sigue haciendo lo que tiene que hacer.

Hace algunos años se creía que lo más valioso era un buen programa y su documentación. Actualmente las organizaciones dedican una gran parte de su presupuesto a diseñar y mantener sus tests.

El testeo de unidades también fuerza al programador a pensar en los distintos casos que la función debe manejar. También tiene la ventaja de que alcanza con enviar los tests una única vez al script, en vez de tener que estar ingresando los mismos datos de testeo una y otra vez a medida que se desarrollar el código.

El código extra que tiene un programa porque facilita el debugging o el testeo se llama scaffolding (andamiaje). El conjunto de tests para chequear un código se llama suite de tests (test suite).

Hay varias formas de hacer testeo de unidades en Python - pero por el momento vamos a ignorar lo que la comunidad Python hace habitualmente, y comenzaremos con dos funciones que escribiremos nosotros mismos. Las utilizaremos para escribir testeos de unidades.

Comencemos con la función valor_absoluto que escribimos en una sección anterior de este capítulo. Habíamos escrito varias versiones de la función, incluyendo la última que era incorrecta y tenía un bug. ¿Qué test hubiera capturado dicho bug? (respuesta: testear el caso valor_absoluto(0))

Primero planeamos nuestros tests. Nos gustaría saber si la función retorna valores correctos cuando el argumento es negativo, cuando es positivo, o cuando es cero. Cuando planemos los tests, nos interesan especialmente los casos de "borde" (aquí, el argumento 0 pasado a la función valor_absoluto es el que corresponde al caso en que la función cambia de comportamiento, y como vimos más temprano en este capítulo, es un punto típico en que el programador puede cometer un error). Por eso es recomendable incluirlo en nuestra suite de tests.

Escribiremos una función auxiliar para chequear los resultados de un test. Toma un argumento booleano y nos muestra un mensaje que indica, o bien que el test pasó o que el test falló. La primera línea del cuerpo (después del docstring de la función) determina mágicamente el número de línea del script en que se hizo el llamado. Esto nos permite imprimir el número de línea del test, que nos ayudará a saber cuál de los tests pasó o falló. (L6_test_suite.py)

def test(exitoso):
    """ Imprime el resultado de un test """
    linenum = sys._getframe(1).f_lineno     # Obtener el número de línea del caller
    if exitoso:
        msg = "Test en línea {0} ok.".format(linenum)
    else:
        msg = "Test en línea {0} FALLÓ.".format(linenum)
    print(msg)

Hay un formateo hecho utilizando la función format que por ahora no explicaremos (lo veremos más adelante). Pero con esta función, podemos proceder a escribir nuestra suite de tests. (L6_test_suite.py)

def test_suite():
    """ Ejecutar la suite de tests para código de este módulo (este archivo)
    """
    test(valor_absoluto(17) == 17)
    test(valor_absoluto(-17) == 17)
    test(valor_absoluto(0) == 0)
    test(valor_absoluto(3.14) == 3.14)
    test(valor_absoluto(-3.14) == 3.14)

test_suite()        # Este es el llamado que ejecuta el test

Podemos luego probarlo con las 3 versiones de la función valor_absoluto (las dos que están bien y la que daba un error). Si lo corremos con una de las dos primeras versiones (las correctas), obtendremos un output como este:

Test en línea 72 ok.
Test en línea 73 ok.
Test en línea 74 ok.
Test en línea 75 ok.
Test en línea 76 ok.

Pero si utilizamos una función incorrecta, como la valor_absoluto_mal_definido vista más arriba, obtendremos:

		Test en línea 72 ok.
		Test en línea 73 ok.
		Test en línea 74 FALLÓ.
		Test en línea 75 ok.
		Test en línea 76 ok.

Y si incluso definimos una versión más incorrecta de valor absoluto, a la que llamaremos valor_absoluto_muy_mal_definido, por ejemplo esta definición: (L6_test_suite.py)

		def valor_absoluto_muy_mal_definido(x):
		    if x < 0:
		        return 1
		    elif x > 0:
		        return x

Obtendremos un reporte de más errores, así:

		Test en línea 78 ok.
		Test en línea 79 FALLÓ.
		Test en línea 80 FALLÓ.
		Test en línea 81 ok.
		Test en línea 82 FALLÓ.

En este caso hay 3 reportes de error (ya que en esta incorrecta versión de valor absoluto, se calculan mal tanto los negativos (con la única excepción del -1) como el 0.

Hay una sentencia que viene con Python, llamada assert, que hace exactamente lo mismo que nuestra test (salvo por el hecho de que el programa se detiene al encontrar el primer error con un assert). Puede ser conveniente leer sobre ella, y utilizarla en lugar de test a futuro.

6.8) Glosario

función booleana, función charlatana, composición de funciones, código muerte, función fructífera, desarrollo incremental, None, valor de retorno
scaffolding (andamiaje), variable temporal, suite de tests (test suite), testeo de unidades

6.9) Ejercicios

Todos los ejercicios de esta sección deberían agregarse a un archivo único. En dicho archivo también deberían agregarse las funciones test y test_suite creadas arriba, y a medida que se avance con los ejercicios, ir agregando los nuevos tests correspondientes a la test suite.

Luego de completar cada ejercicio, confirmar que pase todos los tests.

1) Los 4 puntos cardinales pueden abreviarse con las letras "N", "S", "E", "W". Escribir una función rotar_en_sentido_horario que tome uno de esos 4 puntos cardinales como parámetro, y devuelva el siguiente en el sentido horario. Estos son algunos de los tests que debería pasar: (hacerlo)

		test(rotar_en_sentido_horario("N") == "E")
		test(rotar_en_sentido_horario("W") == "N")

¿Qué hacer si la entrada no es uno de los 4 puntos cardinales? En tal caso devolver None. Así:

		test(rotar_en_sentido_horario(42) == None)
		test(rotar_en_sentido_horario("irrelevante") == None)

2) Escribir una función nombre_del_dia que convierta un entero numerado del 1 al 7 en el nombre de un día. Asumir que el día 1 es "Domingo". Como antes, retornar None si los argumentos pasados a la función no son válidos. Aquí están algunos tests que debería pasar: (hacerlo)

		test(nombre_del_dia(4) == "Miércoles")
		test(nombre_del_dia(7) == "Sábado")
		test(nombre_del_dia(42) == None)

3) Escribir la función inversa numero_del_dia que dado un nombre del día, retorno un número. Y si se le pasa un argumento inválido, devuelve None. (hacerlo)

		test(numero_del_dia("Viernes") == 6)
		test(numero_del_dia("Domingo") == 1)
		test(numero_del_dia(nombre_del_dia(3)) == 3)
		test(nombre_del_dia(numero_del_dia("Jueves")) == "Jueves")
		test(numero_del_dia("Febrero") == None)

4) Escribir una función que permita responder preguntas del tipo: "Hoy es miércoles. Voy a empezar las vacaciones dentro de 19 días. ¿En qué día va a ser?". Por lo tanto, la función ha de tomar un nombre de día y un argumento delta (numérico) y retornar el día resultante. (Pista: usar las dos funciones implementadas en los ejercicios anteriores para facilitar la implementación de ésta) (hacerlo)

		test(sumar_dias("Lunes", 4) == "Viernes")
		test(sumar_dias("Martes", 0) == "Martes")
		test(sumar_dias("Martes", 14) == "Martes")
		test(sumar_dias("Domingo", 100) == "Martes")

5) Funciona tu función con valores negativos de delta? Si lo hace, explicar por qué, y si no lo hace, hacer que funcione. (hacerlo)

Pista: jugar con casos especiales del operador módulo, por ejemplo, ver qué pasa con x % 7 cuando x es negativo

		test(sumar_dias("Domingo", -1) == "Sábado")
		test(sumar_dias("Domingo", -7) == "Domingo")
		test(sumar_dias("Martes", -100) == "Domingo")

Observación: también sería interesante hacer que la función devuelva None en caso de haberse ingresado mal los datos.

6) Escribir una función dias_en_el_mes que recibe el nombre de un mes y devuelve la cantidad de días. Ignorar los años bisiestos. Si se le pasa un argumento inválido, la función debería retornar None. (hacerlo)

		test(dias_en_el_mes("Febrero") == 28)
		test(dias_en_el_mes("Deciembre") == 31)

7) Escribir una función a_segundos que convierta horas, minutos y segundos a un número total de segundos. Algunos tests que debería pasar: (hacerlo)

		test(a_segundos(2, 30, 10) == 9010)
		test(a_segundos(2, 0, 0) == 7200)
		test(a_segundos(0, 2, 0) == 120)
		test(a_segundos(0, 0, 42) == 42)
		test(a_segundos(0, -10, 10) == -590)

8) Extender a_segundos para que pueda manejar valores reales como input. Debería siempre retornar una cantidad entera de segundos (truncando hacia cero). (hacerlo)

		test(a_segundos(2.5, 0, 10.71) == 9010)
		test(a_segundos(2.433, 0, 0) == 8758)

9) Escribir 3 funciones que sean las "inversas" de a_segundos. (hacerlo)

horas_en retorna la cantidad de horas completas contenidas en una cantidad dada de segundos.
minutos_en retorna la cantidad de minutos completos contenidos en una cantidad dada de segundos, luego de que ya se descontaron las horas completas.
segundos_en retorna los segundos sobrantes cuando ya se han descontado las horas y minutos completos.

Se puede asumir que el número total de segundos que se pasará a estas funciones es entero. Algunos casos de testeo:

		test(horas_en(9010) == 2)
		test(minutos_en(9010) == 30)
		test(segundos_en(9010) == 10)

La definición anterior podía parecer un poco confusa, pero los tests dejan bien claro qué es lo que se espera que haga cada función.

Los testeos de unidades muchas veces conllevan el beneficio secundario de aclarar las especificaciones - tenerlo en cuenta al escribir testeos de unidades
Es recomendable la lectura de este artículo que habla sobre inteligencia fluida e inteligencia cristalizada: Fluid vs. Crystallized Intelligence (en inglés)
- Aprender a programar requiere una buena combinación de ambas clases de inteligencia

10) Cuál de estos tests falla? Explicar por qué

		test(3 % 4 == 0)				
		test(3 % 4 == 3)
		test(3 / 4 == 0)				
		test(3 // 4 == 0)
		test(3+4  *  2 == 14)			
		test(4-2+2 == 0)				
		test(len("hello, world!") == 13)

Solución:

		test(3 % 4 == 0)				# FALLA (porque el módulo no da 0)
		test(3 % 4 == 3)
		test(3 / 4 == 0)				# FALLA (porque la división no es entera)
		test(3 // 4 == 0)
		test(3+4  *  2 == 14)				# FALLA (3 + 4*2 no da 14)
		test(4-2+2 == 0)				# FALLA (4 - 2 + 2 no da 0)
		test(len("hello, world!") == 13)

11) Escribir una función comparar que retorne 1 si a > b, 0 si a == b y -1 si a < b (hacerlo)

		test(comparar(5, 4) == 1)
		test(comparar(7, 7) == 0)
		test(comparar(2, 3) == -1)
		test(comparar(42, 1) == 1)

12) Escribir una función hipotenusa que devuelva el tamaño de la hipotenusa de un triángulo rectángulo, dados sus dos catetos (hacerlo)

		test(hipotenusa(3, 4) == 5.0)
		test(hipotenusa(12, 5) == 13.0)
		test(hipotenusa(24, 7) == 25.0)
		test(hipotenusa(9, 12) == 15.0)

13) Escribir una función pendiente(x1, y1, x2, y2) que devuelva la pendiente de la línea entre los puntos (x1, y1) y (x2, y2). Chequear que pase los siguientes tests: (hacerlo)

		test(pendiente(5, 3, 4, 2) == 1.0)
		test(pendiente(1, 2, 3, 2) == 0.0)
		test(pendiente(1, 2, 3, 3) == 0.5)
		test(pendiente(2, 4, 1, 2) == 2.0)

Usar un llamado a pendiente en una nueva función llamada ordenada_en_origen(x1, y1, x2, y2) que retorne la ordenada en el origen de la línea que pasa por los puntos (x1, y1) y (x2, y2) (hacerlo)

		test(ordenada_en_origen(1, 6, 3, 12) == 3.0)
		test(ordenada_en_origen(6, 1, 1, 6) == 7.0)
		test(ordenada_en_origen(4, 6, 12, 8) == 5.0)

Qué se debería retornar en ambas funciones si la recta dada por los 2 puntos es vertical?

14) Escribir una función llamada es_par(n) que reciba un entero como argumento y retorne True si el argumento es un número par y False en caso contrario (hacerlo)

Agrega tus propios tests a la test suite (hacerlo)

15) Escribir ahora la función es_impar(n) e incluirle una unidad de testeo también. (hacerlo)

Luego, modificarla para que utilice un llamado a es_par para determinar si su argumento es impar, y verificar que siga pasando el test. (hacerlo)

16) Escribir una función es_factor(n) que pase los tests siguientes: (hacerlo)

		test(es_factor(3, 12))
		test(not es_factor(5, 12))
		test(es_factor(7, 14))
		test(not es_factor(7, 15))
		test(es_factor(1, 15))
		test(es_factor(15, 15))
		test(not es_factor(25, 15))

Un rol importante de las unidades de testeo es que pueden servir como "especificaciones" no ambiguas de lo que se espera.

Estos casos de testeo responden a la pregunta: ¿debemos considerar a 1 y 15 como factores de 15?

17) Escribir es_multiplo para satisfacer estos testeos: (hacerlo)

		test(es_multiplo(12, 3))
		test(es_multiplo(12, 4))
		test(not es_multiplo(12, 5))
		test(es_multiplo(12, 6))
		test(not es_multiplo(12, 7))

Observación: no especifica qué hacer cuando la entrada es incorrecta, y si debemos considerar a los números negativos como entradas válidas
Puedes encontrar un modo de utilizar es_factor para definir (implementar) a es_multiplo?

18) Escribir la función f2c(t) que retorna el valor entero del grado Celsius más cercano a una temperatura dada en Fahrenheit. (hacerlo)

Pista: puede ser útil utilizar la función round. Imprimiendo round.__doc__ en el shell de Python o pidiendo ayuda sobre la función round se puede aprender más sobre ella.

		test(f2c(212) == 100)     	# Punto de ebullición del agua
		test(f2c(32) == 0)        	# Punto de congelación del agua
		test(f2c(-40) == -40)     	# Curiosa coincidencia?
		test(f2c(36) == 2)
		test(f2c(37) == 3)
		test(f2c(38) == 3)
		test(f2c(39) == 4)

19) Ahora hacer lo opuesto: escribir la función c2f(t) que convierte Celsius a Fahrenheit: (hacerlo)

		test(c2f(0) == 32)
		test(c2f(100) == 212)
		test(c2f(-40) == -40)
		test(c2f(12) == 54)
		test(c2f(18) == 64)
		test(c2f(-48) == -54)